프림 알고리즘
- MST(Minimum Spanning Tree, 최소 신장 트리)
- 프림 알고리즘은 정점을 추가하면서 트리를 확장하는 방법
- 프림 알고리즘은 하나의 시작점을 잡고 시작점과 연결된 정점들에 대해 가장 가중치가 작은 간선부터 연결해주면서 최소 스패닝 트리를 만들어 나가는 알고리즘
- 이때 가장 작은 간선부터 간선을 연결하되, 연결하는 도중 사이클이 생기게 된다면 가중치가 작은 간선이어도 무시하여야 한다.
- 한 정점을 기준으로 가능한 작은 가중치의 간선을 사용해서 모든 정점을 연결하는 트리를 만든다. 즉, 최소의 간선 값만 사용해서 모든 정점을 연결한다.
- BFS와 같이 시작점을 기준으로 간선이 확장해나가는 방식
- 대신 Prim’s 알고리즘은 간선에 가중치가 있으며, 최소한의 비용을 갖는 트리를 만들어야 한다는 점에서 차이가 있다.
풀이
1
2
3
4
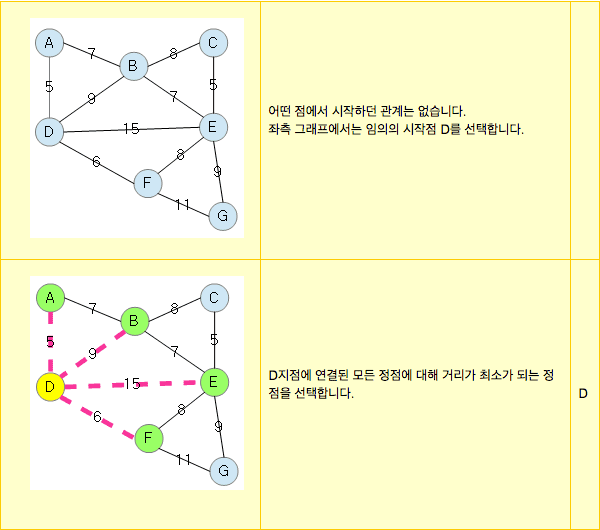
0. 어떤 점에서 시작하던 상관없다.
1. 그래프에서 임의의 하나의 정점을 선택한다.
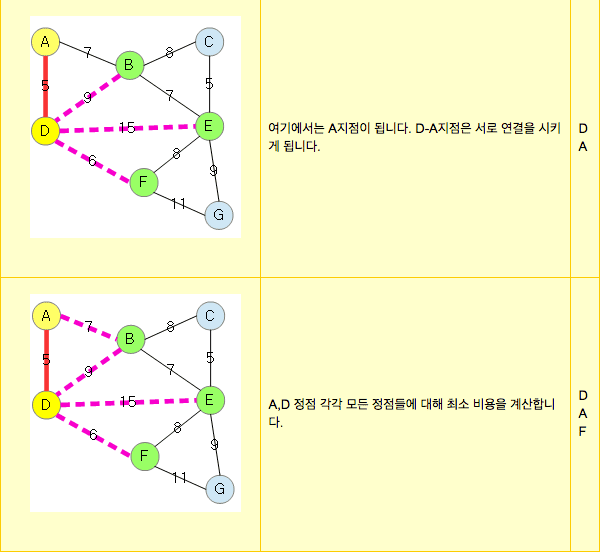
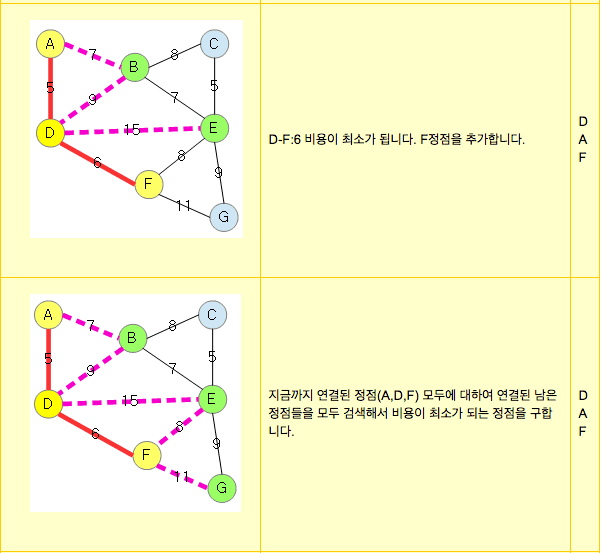
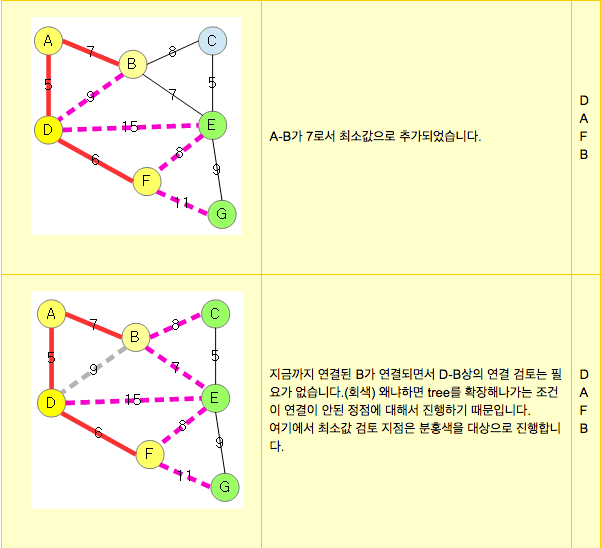
2. 선택한 정점과 인접하는 정점들중 최소 비용의 간선이 존재하게되는 정점을 선택한다.
3. 1,2 과정을 반복 하여 모든 정점이 선택될까지 한다.
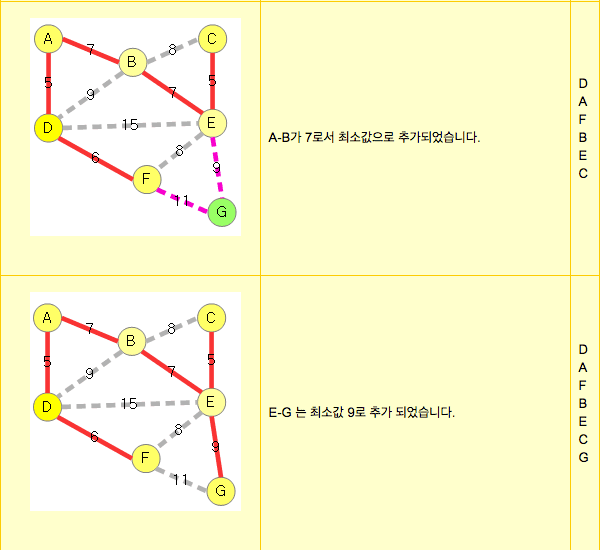
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <functional>
#include <limits.h>
#define MAX_NODE 10001
using namespace std;
typedef pair<int, int> pii;
int V, E;
bool visit[MAX_NODE];
vector<int> d[MAX_NODE]; //최단거리
vector<pii> vc[MAX_NODE];
void dijikstra(int start){
visit[start] = true;
// 우선 순위 큐(최소 힙)
priority_queue<pii, vector<pii>, greater<pii>> pq;
// 1번 정점을 시작점으로 한다.
for (int i = 0; i < vc[start].size(); i++)
{
// 정점과 가중치를 priority_queue에 넣어준다.
int next = vc[start][i].first;
int nextCost = vc[start][i].second;
pq.push(pii(nextCost, next));
}
int ans = 0;
while (!pq.empty())
{
/*
모든 정점을 우선 순위 큐로 확인하니 logV,
그 정점들에 대해 간선을 확인하니 E, 따라서 O(ElogV)가 된다.
*/
int here = pq.top().second; //정점
int hereCost = pq.top().first; //가중치
pq.pop();
// 이미 방문한 정점은 무시한다.-> 사이클 방지
if (visit[here])
continue;
visit[here] = true;
ans += hereCost;
// 다음 정점을 우선순위 큐에 넣어준다.
for (int i = 0; i < vc[here].size(); i++)
{
int there = vc[here][i].first;
int thereCost = vc[here][i].second;
pq.push(pii(thereCost, there));
}
}
printf("%d", ans); //최소 가중치
}
int main()
{
scanf("%d %d", &V, &E);
for(int i=0; i < V ; i++){
d[i]=INT_MAX, visit[i]=0;
}
for (int i = 0; i < E; i++)
{
int from, to, val;
scanf("%d %d %d", &from, &to, &val);
vc[from].push_back(pii(to, val));
vc[to].push_back(pii(from, val));
}
dijkstra(0);
return 0;
}
출처: https://www.crocus.co.kr/733 [Crocus]
크루스칼 알고리즘 vs 프림 알고리즘
그렇다면 언제 크루스칼 알고리즘을 쓰고, 언제 프림 알고리즘을 쓰면 좋을까?
이에따른 정답은 시간 복잡도로 생각해 보면 좋을 것 같다.
크루스칼 알고리즘 시간 복잡도 :: O(Elog2E)
프림 알고리즘 시간 복잡도 :: O(Elog2V)
결국, 간선의 개수가 작은 경우에는 크루스칼 알고리즘을, 간선의 개수가 많은 경우에는 프림 알고리즘이 더 좋다는 것이 자명하다.
###
참고
https://goodgid.github.io/Prim-Algorithm/
https://www.crocus.co.kr/733 [Crocus]